概述
在計算機科學中,AVL樹是最先發明的自平衡二叉查找樹。AVL樹得名於它的發明者 G.M.Adelson-Velsky和E.M.Landis,他們在1962年的論文《An algorithm for the organization of information》中發表了它。節點計算
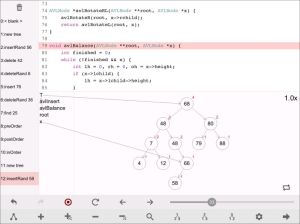 AVL
AVL 最少節點數 n 如以斐波那契數列可以用數學歸納法證明:
Nh=F【h+2】 - 1 (F【h+2】是 Fibonacci polynomial 的第h+2個數)。
即:
N0 = 0(表示 AVL Tree 高度為0的節點總數)
N1 = 1(表示 AVL Tree 高度為1的節點總數)
N2 = 2(表示 AVL Tree 高度為2的節點總數)
Nh=N【h− 1】 +N【h− 2】 + 1 (表示 AVL Tree 高度為h的節點總數)
換句話說,當節點數為 N 時,高度 h 最多為 節點的平衡因子是它的右子樹的高度減去它的左子樹的高度。帶有平衡因子 1、0 或 -1 的節點被認為是平衡的。帶有平衡因子 -2 或 2 的節點被認為是不平衡的,並需要重新平衡這個樹。平衡因子可以直接存儲在每個節點中,或從可能存儲在節點中的子樹高度計算出來。
操作
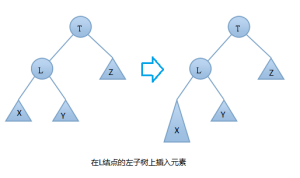 AVL
AVL 假設由於在二叉排序樹上插入結點而失去平衡的最小子樹根結點的指針為a(即a是離插入點最近,且平衡因子絕對值超過1的祖先結點),則失去平衡後進行進行的規律可歸納為下列四種情況:
單向右旋平衡處理RR:由於在*a的左子樹根結點的左子樹上插入結點,*a的平衡因子由1增至2,致使以*a為根的子樹失去平衡,則需進行一次右旋轉操作;
單向左旋平衡處理LL:由於在*a的右子樹根結點的右子樹上插入結點,*a的平衡因子由-1變為-2,致使以*a為根的子樹失去平衡,則需進行一次 左旋轉操作;
雙向旋轉(先左後右)平衡處理LR:由於在*a的左子樹根結點的右子樹上插入結點,*a的平衡因子由1增至2,致使以*a為根的子樹失去平衡,則需進行兩次旋轉(先左旋後右旋)操作。
雙向旋轉(先右後左)平衡處理RL:由於在*a的右子樹根結點的左子樹上插入結點,*a的平衡因子由-1變為-2,致使以*a為根的子樹失去平衡,則需進行兩次旋轉(先右旋後左旋)操作。
插入
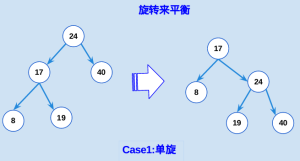 AVL
AVL 刪除
從AVL樹中刪除可以通過把要刪除的節點向下旋轉成一個葉子節點,接著直接剪除這個葉子節點來完成。因為在旋轉成葉子節點期間最多有 log n個節點被旋轉,而每次 AVL 旋轉耗費恆定的時間,刪除處理在整體上耗費 O(log n) 時間。查找
在AVL樹中查找同在一般BST完全一樣的進行,所以 耗費 O(log n) 時間,因為AVL樹總是保持平衡的。不需要特殊的準備,樹的結構不會由於查詢而改變。(這是與伸展樹查找相對立的,它會因為查找而變更樹結構。)代碼實現
public class AVLTree > {private AVLNode root;
public AVLTree() {root = null;}
/*** Check if given item x is in the tree.*/
public boolean contains(T x) {return contains(x, root);}
/*** Internal method to check if given item x is in the subtree.*
* @param x* the given item to check.
* @param t* the node that roots the subtree.*/
private boolean contains(T x, AVLNode t) {while (t != null)
{int compareResult = x.compareTo(t.element);
if (compareResult 0)
t = t.right;
else
return true;}
return false;}
/*** Insert a new item to the AVL tree.*
* @param x
* the item to insert.*/
public void insert(T x) {
root = insert(x, root);}
/*** Internal method to insert into a subtree.*
* @param x
* the item to insert.
* @param t
* the node that roots the subtree.
* @return the new root of the subtree.*/
private AVLNode insert(T x, AVLNode t) {
if (t == null)
return new AVLNode (x);
int compareResult = x.compareTo(t.element);
if (compareResult 0)
t = rotateWithRightChild(t);
else
t = doubleWithRightChild(t);}
else;
t.height = Math.max(height(t.left), height(t.right)) + 1;
return t;}
/*** Return the height of root t, or -1, if null.*
* @param t
* an AVLNode.
* @return the height.*/
private int height(AVLNode t) {
return t == null ? -1 : t.height}
/*** Single rotation (left-left). Update height, then return new root.*/
private AVLNode rotateWithLeftChild(AVLNode z) {
AVLNode y = z.left;
z.left = y.right;
y.right = z;
z.height = Math.max(height(z.left), height(z.right)) + 1;
y.height = Math.max(height(y.left), z.height) + 1;
return y;}
/*** Single rotation (right-right). Update height, then return new root.*/
private AVLNode rotateWithRightChild(AVLNode z) {
AVLNode y = z.right;
z.right = y.left;
y.left = z;
z.height = Math.max(height(z.left), height(z.right)) + 1;
y.height = Math.max(height(y.right), z.height) + 1;
return y;}
/*** Double rotation (left-right).*/
private AVLNode doubleWithLeftChild(AVLNode z)
{z.left = rotateWithRightChild(z.left);
return rotateWithLeftChild(z);}
/*** Double rotation (right-left).*/
private AVLNode doubleWithRightChild(AVLNode z) {
z.right = rotateWithLeftChild(z.right);
return rotateWithRightChild(z);}
/**Remove item x.*/
public void remove(T x)
{root = remove(x, root);}
/*** Remove item x from subtree t.
* @param x the item to be removed.
* @param t the node that roots the subtree.
* @return the new root of the subtree.*/
private AVLNode remove(T x, AVLNode t) {
if (t == null)
return t;
int compareResult = x.compareTo(t.element);
if (compareResult height(t.left.right))
t = rotateWithLeftChild(t);
else
t = doubleWithLeftChild(t);}
else if (t.left != null && t.right != null)
{t.element = findMin(t.right).element;
t.right = remove(t.element, t.right);
if (height(t.left) - height(t.right) == 2)
if (height(t.left.left) > height(t.left.right))
t = rotateWithLeftChild(t);
else
t = doubleWithLeftChild(t);}
else
{t = (t.left != null) ? t.left : t.right;}
if (t != null)
t.height = Math.max(height(t.left), height(t.right)) + 1;
return t;}
public T findMin()
{if (isEmpty())
return null;
return findMin(root).element;}
private AVLNode findMin(AVLNode t) {
while (t.left != null)
t = t.left;
return t;}
public T findMax()
{if (isEmpty())
return null;
return findMax(root).element;}
private AVLNode findMax(AVLNode t) {
while (t.right != null)
t = t.right;
return t;}
public void makeEmpty()
{root = null;}
public boolean isEmpty()
{return root == null;}
/** Internal class AVLNode */
private static class AVLNode
{T element;
AVLNode left;
AVLNode right;
int height;
public AVLNode(T element)
{this(element, null, null);}
public AVLNode(T element, AVLNode left, AVLNode right)
{this.element = element;
this.left = left;
this.right = right;
this.height = 0;}}}
AVL
單元編碼
編碼就是對信息進行轉換,使之獲得適合於記憶 系統的形式的加工過程(Encoding)。經過編碼所產生的具體的信息形式叫做代碼(Code)。⑴回憶錯誤實驗表明:人們在回憶時產生錯誤主要發生在聲音相近的字母混淆上。說明短時記憶的信息代碼主要是聲音代碼或聽覺代碼。
⑵即使使用視覺材料作為刺激,其代碼也仍有聽覺性質,在短時記憶中出現形聲轉換,而以聲音形式貯存。
⑶鑒於字母、字詞的聽覺代碼和口語代碼都是不同形式的言語 代碼,因此,常將聽覺的(Auditory)、口語的(Verbal)、言語的(Languistic)代碼聯合起來,稱之為A.V.L單元。
![AVL[二叉查找樹] AVL[二叉查找樹]](/img/d/090/nBnauM3XxEDN5gDMwYzNxAjN0QTMwczN5cDNzQTNwAzMwIzL2czL2QzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg)
